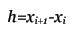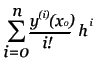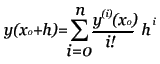| Все для программирования. |
| начало | почта | статьи | файлы | ссылки | сайты | RSS | о нас | опубликовать | оформление | авторы | друзья | реклама |
|
Каталог статей
|
Статья
Задача Коши для обыкновенных дифференциальных уравнений. Здесь будут рассмотрены различные методы численного решения дифференциальных уравнение. Но, для начала, дам краткое пояснение того, что это за уравнения ... Примечание: К сожалению, я не могу изложить здесь все основы мат анализа, поэтому, если вы не знакомы с такими понятиями как интегрирование и дифференцирование, вам эту статью читать незачем. Дифференциальное уравнение отличается от обычного тем, что в нём, помимо переменной x присутствует зависящая от него функция y, а также её производные. Общий вид: F(x) = 0 - обычное уравнение, F(x,y,y',y'',...) = 0 - дифференциальное уравнение. Порядок уравнения определяется наибольшим порядком производной. Решением уравнения является функция y = f(x). Задача Коши для диф. уравнения n-го порядка - это нахождение такого решения, которое будет удовлетворять заданным начальным условиям. 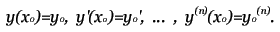 Далее, будут приведены численные методы решения задачи Коши для обыкновенных дифференциальных уравнений 1-го порядка: F(x,y,y') = 0 или y' = f(x,y). Содержание данной статьи: Решение с помощью формулы Тейлора. Это наиболее простой и понятный способ. Пусть необходимо решить уравнение: 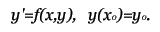 Для того, что бы получить производные высших порядков для формулы Тейлора, 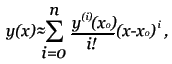 продифференцируем наше уравнение по x: 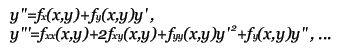 После подстановки начальных условий получим значения высших производных: 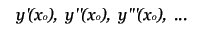 Алгоритм вычисления:
Метод прост, но требует вычисления N * (N + 1) / 2 значений различных функций на каждом шаге. Методы Рунге-Кутта. Пусть известно значение y(x) тогда y(x + h) находится из такого равенства: 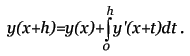 Заменив интеграл на hy'(x) получим: 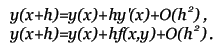 Где y' = f(x,y) - наше диф. уравнение,   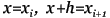 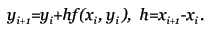 Для большей точности, аппроксимируем интеграл по формуле трапеции: 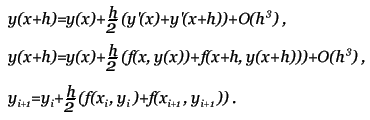 Адамса, на порядок погрешности которой, эта подстановка не влияет: 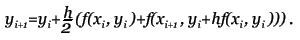 Можно заменить интеграл по формуле прямоугольников, тогда расчётная формула выглядит так: 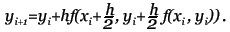 Эти формулы относятся к семейству методов Рунге-Кутта, имеющих следующий вид: 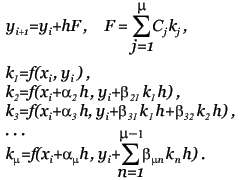 Давать подробное описание этим методам я не буду, если кому интересно, пусть читает соответствующую литературу. Приведу самые употребительные соотношения: Для методов 2-го порядка 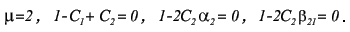 Метод 3-го порядка 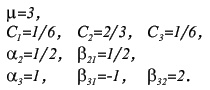 Метод 4-го порядка 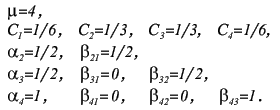 Надеюсь в данном случае, алгоритм расчета понятен без лишних слов. Конечно-разностные методы. В отличии от предыдущих, конечно-разностные методы относятся к k-шаговым, и интегрирование производится с постоянным шагом (в предыдущих значение h можно было свободно менять). Основной вид конечно-разностных методов, или конечно-разностных схем таков: 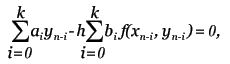 но из ряда причин используют в основном только такие методы 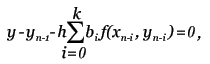 Они называются методами Адамса. Явные формулы Адамса: 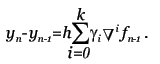 Неявные формулы Адамса: 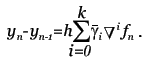 Коэффициенты: 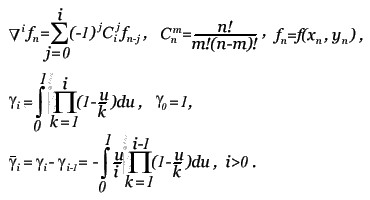 Для расчёта через неявную формулу, в неё подставляют значение найденное по явной формуле. В конце статьи приведена программа расчёта по неявной формуле Адамса с i = 4. Примеры вычислений. Для начала возьмем простенькое уравнение: 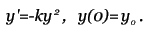 Решение с помощью формулы Тейлора: Находим производные высших порядков (ограничимся 4-ым): 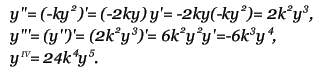 Самый простой цикл расчета написанный на Си выглядит так: Код: (C) h = 0.0001; x = x1; i = 0; while(x) { y[i]=y0; y[i]+=y1(t)*h; y[i]+=y2(t)*h*h/2.0; y[i]+=y3(t)*h*h*h/6.0; y[i]+=y4(t)*h*h*h*h/24.0; y0=y[i]; x+=h; i++; } [x1;x2] - область интегрирования, y[i] - результаты вычислений, y0 = v(0) - начальные условия, y1(t) ... y4(t) - производные. Более подробно рассмотрим решение уравнения: 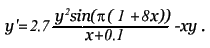 Пусть надо построить зависимость y(x) и найти точку с максимальным значением y на отрезке [0,1], если y(0) = 1. В этом случае находить производные довольно сложно, поэтому лучше будет использовать методы Рунге-Кутта или конечноразностные схемы. Вот пример программы выполняющей расчет данного уравнения по неявной формуле Адамса с i = 4: Код: (C) // Написано под "Turbo C++ v3.0", запускать в эмуляции MS-DOS #include <bios.h> #include <bios.h> #include <stdio.h> // Вывод точки #define SetPixel(X,Y,C) *((unsigned char far *)(0xA0000000L+0x0140*(Y)+(X)))=((unsigned char)(C)) // Шаг интегрирования double h=0.0001; // Наше диф. уравнение double f(double X, double Y) { double F; F=2.70*Y*Y*sin(M_PI*(0.50+8.00*X))/(X+0.10)-X*Y; return(F); } // факториал double NF(unsigned int N) { unsigned long int P=1.00; if(!N) return P; while(N) { P*=N; N--; } return (double)P; } // коэффициенты бинома Ньютона double Cnm(unsigned int N, unsigned int M) { return NF(N)/(NF(M)*NF(N-M)); } // дополнительная функция double DF(double X, double *Y, unsigned int N) { unsigned int I; double S=0.00,Sign=1.00; for(I=0x00;I<=N;I++) { S+=Sign*Cnm(N,I)*f(X-h*(double)I,*(Y+0x03-I)); Sign=-Sign; } return S; } // ну, если вы не знаете, что такое main(), то зачем это читаете? void main() { double X1=0.00,X2=1.00,Y0=1.00; double X,DY; double Y[0x04]; unsigned int x,y,i; double MaxX,MaxY; // коэффициенты, см. Конечно разносные методы double G[0x04]={ 1.00, 1.00/2.00, 5.00/12.00, 3.00/8.00 }; double g[0x04]={ 1.00,-1.00/2.00,-1.00/12.00,-1.00/24.00 }; // точка максимального значения MaxX=X1; MaxY=Y0; // Включение графического режима 320*200*256 asm MOV AX,0x0013; asm INT 0x10; // Подставляем начальные условия и производим расчет // первых 4-ёх значений по неявной формуле Адамса 2-го порядка точности X=X1; Y[0x00]=Y0; Y[0x01]=Y[0x00]+h*(f(X,Y[0x00])+f(X+h,Y[0x00]+h*f(X,Y[0x00])))/2.00; X+=h; Y[0x02]=Y[0x01]+h*(f(X,Y[0x01])+f(X+h,Y[0x01]+h*f(X,Y[0x01])))/2.00; X+=h; Y[0x03]=Y[0x02]+h*(f(X,Y[0x02])+f(X+h,Y[0x02]+h*f(X,Y[0x02])))/2.00; X+=h; // основной расчетный цикл while(X < X2) { // рассчитываем по явной формуле DY=0.00; for(i=0x00;i<0x04;i++) DY+=G[i]*DF(X,Y,i); DY*=h; // перемещаемся на шаг вперед for(i=0x00;i<0x03;i++) Y[i]=Y[i+0x01]; Y[0x03]+=DY; X+=h; // две итерации на основе неявной формулы DY=0.00; for(i=0x00;i<0x04;i++) DY+=g[i]*DF(X,Y,i); DY*=h; Y[0x03]=Y[0x02]+DY; DY=0.00; for(i=0x00;i<0x04;i++) DY+=g[i]*DF(X,Y,i); DY*=h; Y[0x03]=Y[0x02]+DY; // проверяем максимальное значение if(MaxY < Y[0x03]) { MaxY=Y[0x03]; MaxX=X; } // вывод на экран x=0x0140*(X/(X2-X1)); if(x<0x140) { DY=f(X,Y[0x03]); y=0xC8*(0.50-0.0014*DY); if(y<0xC8) SetPixel(x,y,0x0D); y=0xC8*(1.00-0.1*Y[0x03]); if(y<0xC8) SetPixel(x,y,0x0E); } } // пауза bioskey(0x00); // выкл. графического режима asm MOV AX,0x0003; asm INT 0x10; // Вывод данных printf("Max - %.14g,%.14gn",MaxX,MaxY); // пауза bioskey(0x00); } В результате имеем такой график: 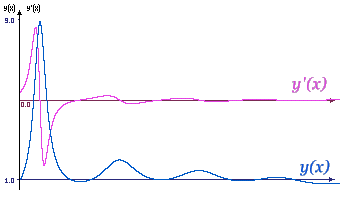 И такие значения максимума:
Надеюсь, прочитав эту статью вы уяснили, что в численных методах нет ничего сложного, не смотря на то, что в книгах это выглядит весьма ужасно. Автор: Vorlon |
| начало | почта | статьи | файлы | ссылки | сайты | RSS | о нас | опубликовать | оформление | авторы | друзья | реклама |