| Все для программирования. |
| начало | почта | статьи | файлы | ссылки | сайты | RSS | о нас | опубликовать | оформление | авторы | друзья | реклама |
|
Каталог статей
|
Статья
Теоретические основы реляционных баз данных. Предисловие Как уже упоминалось в предыдущей статье, на поверхностном уровне реляционную базу данных можно представить себе как набор взаимосвязанных таблиц, содержащих данные. (К слову сказать, ранние примитивные реляционные СУБД, некоторые из которых дожили и до настоящего времени, по сути таковым набором и являются; средства, которые превращают реляционную БД из набора таблиц в мощное средство хранения и обработки данных, в них отсутствуют и должны реализовываться разработчиком приложения самостоятельно). Но такой взгляд на предмет все же является излишне примитивным и упрощенным. Приложения для работы с электронными таблицами возникли достаточно давно и имеют свою определенную нишу. Полагаю, что большинство персональных компьютеров, работающих под управлением ОС семейства MS Windows, оснащено программой табличного процессора Excel. Тем не менее Excel, хотя и работает с табличными данными, не является СУБД. Читателю следует обратить внимание на основные моменты, которые отличают реляционные СУБД от электронных таблиц, и не смешивать эти понятия. Ранее упоминалось, что успех реляционной модели не в последнюю очередь определялся солидной теоретической базой, которая строится на базе реляционной алгебры, математической логики, исчисления предикатов и некоторых других разделов математики. Объем данной статьи не позволит дать исчерпывающее руководство по данному предмету, да в соответствующих материалах и нет недостатка в настоящий момент. Но не имея представления о теории, невозможно спроектировать надежную и эффективную БД с возможностью гибкой обработки данных. Цель данной статьи дать читателю начальные знания, необходимые для понимания механизмов работы реляционных СУБД. Первый пример базы данных Попробуем построить простейшую базу данных, например, по домашней библиотеке. Нас будут интересовать следующие данные о книге: Номер книги в каталоге
Для примера взял первые попавшиеся книги, до которых смог дотянуться на рабочем столе. Вот что у меня получилось:
Разумеется, помимо этих характеристик, книги обладают и другими, но в данной задаче ограничимся этим набором. В дальнейшем будем называть эти характеристики атрибутами. Если мы решили представить нашу базу в табличном виде, очевидно, что каждый атрибут соответствует столбцу таблицы, а полная информация об одной книге строке таблицы. Типы атрибутов и домены. Очевидно, что, несмотря на разнообразие допустимых значений атрибута, не все из них являются допустимыми. Например, год издания должен быть целым числом, номер книги неотрицательным целым, значения остальных атрибутов могут быть представлены строковыми значениями. Таким образом, каждый атрибут имеет свой тип, который ограничивает множество принимаемых атрибутом значений. Примечание. Вообще говоря, при строгом математическом подходе следует различать сами атрибуты и их значения. Но многие авторы для краткости опускают эти тонкости там, где различие очевидно из контекста. Я тоже последую их примеру и буду писать атрибут равен тому-то вместо значение атрибута равно тому-то, если это не приведет к путанице. Набор типов, поддерживаемых реляционными СУБД, включает в себя простые (атомарные) типы данных, знакомые нам по большинству языков программирования. В них входят: логический (булевский) тип, числовые типы целочисленный и с плавающей точкой, дата/время, а также строковый тип. Многие СУБД поддерживают также тип BLOB произвольный массив байтов. СУБД никак не интерпретирует внутреннюю структуру BLOB, и его использование полностью определяется логикой прикладной программы, получающей эти значения. В виде BLOB можно, например, хранить фотографию сотрудника в базе данных отдела кадров или демо-ролик фильма в каталоге видеотеки. Помимо ограничений типа, на значения атрибутов могут накладываться дополнительные ограничения. Скажем, в нашем примере с библиотечным каталогом крайне подозрителен, например, будет год издания книги ранее 1400, ибо до рождения Гуттенберга книги никто не печатал. Если вы не коллекционируете египетские папирусы или клинопись Междуречья, скорее всего, появление подобной записи в базе является результатом ошибки при вводе либо сбойного сектора на диске. Появление книги с годом издания позже нынешнего тоже довольно подозрительно. Подмножество значений данного типа, допустимых для данного атрибута, называется доменом. В некоторых случаях определить домен довольно легко; например, для атрибута пол человека достаточно перечислить два допустимых значения. В случае с годом издания задача немного сложнее, но тоже решаема. Не труднее определить домен для атрибута номер в каталоге книги: очевидно, что это должно быть положительное целое число, и при нумерации по порядку маловероятно, что для личной библиотеки оно превысит 10.000. В других случаях формально определить домен довольно проблематично. Например, атрибут название книги должен быть осмысленным набором символов, произвольный набор тут недопустим. В то же время я не знаю способа формально определить осмысленность названия книги: ни перечисление допустимых значений, ни алгоритм распознавания тут не помогут. Таким образом, если тип это физическая характеристика множества значений атрибута, допускающая четкое формальное определение, то домен скорее логическое понятие, иногда допускающее интуитивное описание. От интуитивного подхода - к формальному В нашем первом примере мы пользовались в основном интуитивными понятиями для объяснения таких сущностей, как атрибут, домен и т.д. Однако неоднократно упоминалось, что красота и мощь реляционного подхода в математической платформе, на которой он базируется. Придется и нам немного погрузиться в основы реляционной алгебры. Примечание. В дальнейшем изложении я буду вынужден время от времени использовать элементы теории множеств. Постараюсь не злоупотреблять ими, но там, где без этого никак нельзя обойтись без ущерба для ясности описания, они все же будут встречаться. Те из читателей, кто не знаком с предметом или подзабыл его, могут ознакомиться со статьей по адресу http://www.citforum.ru/database/dblearn/dblearn01.shtml, в которой основы теории множеств изложены сжато и доступно. Итак, от частных примеров переходим к общему формальному описанию.Если A1, A2, An множества, то подмножество R их декартова произведения A1 * A2 * * An называется отношением степени n. Каждое из множеств Ai представляет собой домен. Примечание. Поскольку Гром просил при написании статей не злоупотреблять специальными символами, я по возможности постараюсь воспроизводить формулы, пользуясь стандартным символьным набором. Не обессудьте, если вид формул будет несколько отличаться от общепринятого, смысл при этом нисколько не пострадает. Отношение определяется заголовком, который представляет собой множество атрибутов. Например, для нашего простейшего примера схема выглядит следующим образом: Книга(Номер_книги, Авторы, Название, Издательство, Год_издания) Примечание. Строго говоря, для каждого из атрибутов следовало бы указывать его домен, т.е. представлять атрибут в виде пары <Имя_атрибута: Имя_домена>; однако на практике зачастую имя атрибута однозначно определяет одноименный домен, и запись можно упростить. Тело отношения R является множеством упорядоченных наборов вида (a1, a2, an), где каждое ai принадлежит множеству Ai. Подобные наборы принято называть кортежами. Следует заметить, что, хотя кортежи весьма напоминают строки таблицы, а тело отношения саму таблицу, полной аналогии здесь нет. По своей природе кортежи не являются упорядоченными. Забегая вперед, добавлю, что реляционные базы данных, хотя и позволяют упорядочивать результаты запросов некоторым образом, тем не менее не гарантируют, что сами хранимые данные как-то упорядочены. Другими словами, если мы записываем данные в реляционную базу в какой-то последовательности, не стоит рассчитывать на то, что получить их обратно мы сможем в том же порядке. Операции, допустимые над отношениями Все определения, введенные до сих пор, казалось бы, только затуманивают и без того интуитивно ясные понятия, на базе которых мы безо всякой теории могли бы построить картотеку книг, скажем, в том же Excelе. Для чего понадобилось притягивать сюда теорию множеств? Ответ прост мы ввели математический аппарат для того, чтобы иметь возможность не только определить данные, но и манипулироватьими. Чтобы иметь возможность обрабатывать данные, нужно вооружиться набором операцийнад отношениями. Эти операции используют отношения в качестве операндов, и результатом их также является отношение. Логично будет разделить их на две группы операций: теоретико-множественные и собственно реляционные. Теоретико-множественные операции Поскольку реляционная теория базируется на теории множеств, естественно предположить, что теоретико-множественные операторы можно применять и для отношений. Как мы увидим далее, это предположение вполне справедливо. Итак, рассмотрим четыре оператора:
Объединение Оператор объединения применим только к отношениям, совместимым по типу, т.е. к отношениям, имеющим одно и то же множество атрибутов, причем одноименные атрибуты определены на одинаковых доменах. Операция объединения отношений A и B обозначается следующим образом: A UNION B Результат операций теории множеств можно сделать нагляднее посредством диаграмм Эйлера-Венна. Построим диаграмму для операции объединения: 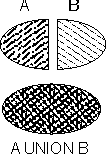 Мы видим, что результатом объединения двух множеств является множество, включающее в себя все элементы исходных множеств. В случае, когда A и B отношения, результатом их объединения является отношение, заголовок которого совпадает с заголовками A и B, а тело включает кортежи из обоих отношений (исключая возможные дубликаты). Например, отношение COMP_BOOKS содержит данные по компьютерным книгам в библиотеке, а отношение MATH_BOOKSпо математическим книгам. Отношение, являющееся результатом оператора (COMP_BOOKS UNION MATH_BOOKS), содержит перечень книг из обоих разделов, причем книги, включенные в оба раздела (например, по численным методам), будут представлены в результирующем отношении в единственном экземпляре. Пересечение Для этого оператора отношения-операнды также должны быть совместимы по типу. Обозначается пересечение следующим образом: A INTERSECT B Диаграмма для пересечения:  Результатом пересечения двух множеств является множество, элементы которого принадлежат одновременно обоим множествам. В случае пересечения двух отношений результат отношение, заголовок которого совпадает с заголовками исходных отношений, а тело включает кортежи, имеющиеся в обоих отношениях. Если продолжить пример с библиотекой, то оператор (COMP_BOOKS INTERSECT MATH_BOOKS) определяет множество книг, включенных в оба раздела одновременно. Вычитание Как и в предыдущем случае, отношения-операнды должны быть совместимы по типу. Обозначение вычитания: A MINUS B Продолжая иллюстрацию для пересечения множеств, изобразим их разность графически:  Как видно на диаграмме, результирующее множество состоит из элементов, принадлежащих A и не принадлежащих B. Нетрудно догадаться, что применительно к отношениям эта операция дает отношение, заголовок которого совпадает с заголовками исходных отношений, а тело включает все кортежи первого отношения, не включенные во второе. Возвращаясь к примеру с библиотекой, заметим, что оператор (COMP_BOOKS MINUS MATH_BOOKS) выбирает все компьютерные книги, которых нет в математическом разделе. Декартово произведение Для декартова произведения двух множеств нарисовать наглядную диаграмму довольно-таки затруднительно, во всяком случае, для меня. Поэтому придется ограничиться словесным описанием этой операции в применении к отношениям. Если даны два отношения A и B, то их декартовым произведением является отношение, заголовок которого образован сцеплением заголовков исходных отношений, а тело сцеплением кортежей этих отношений. Обозначается эта операция так: A TIMES B В отличие от предыдущих операций, совместимости по типу исходных отношений не требуется. Более того, если отношения содержат атрибуты с одинаковыми именами, атрибут одного из отношений придется переименовать, чтобы избежать неоднозначности имен в результирующем отношении. Операция кажется гораздо причудливее, чем три предыдущих. Следует добавить, что и особой самостоятельной ценности она не имеет. Применяется она обычно только в сочетании с реляционными операциями. Реляционные операции Для данной группы операций, пожалуй, я бы затруднился привести наглядное графическое представление. Отложим диаграммы и ограничимся словесным описанием. Выборка Операция выборки это некоторое горизонтальное сечение нашего отношения, т.е. множество кортежей, являющееся подмножеством исходного отношения. Обозначение выборки: A WHERE c Здесь: A исходное отношение, c некоторое условие; результатом выборки является отношение, заголовок которого совпадает с заголовком исходного отношения, а тело является множеством кортежей, при подстановке атрибутов которых в заданное условие оно принимает истинное значение. Простейший пример: Books WHERE (publisher = БХВ) - множество всех книг в библиотеке, изданных БХВ. В реальных выборках условие может быть весьма изощренным, но сути операции это не меняет. Проекция Проекция напоминает выборку в том плане, что тоже представляет сечение отношения, но уже вертикальное. Если вновь прибегнуть к представлению отношения в виде таблицы, то выборку можно представить себе как вычеркивание некоторых строк из таблицы, а проекцию как вычеркивание некоторых столбцов. Обозначается операция проекции так: A[W, X, , Y, Z] A - исходное отношение, подвергающееся проекции. В квадратных скобках задается список атрибутов, которые присутствуют в результирующем отношении. Заголовок отношения A представляет собой множество атрибутов (W, X, , Y, Z), а тело множество кортежей (w, x, , y, z), для каждого из которых в исходном отношении найдется соответствующий кортеж с совпадающим значением атрибута. Выражаясь менее запутанно, в выходном отношении присутствуют все строки исходного и только заданные столбцы. Пример: составить отчет обо всех имеющихся в библиотеке книгах вида Автор Название. Books [author, title] Соединение Хотя соединение рассматривается как отдельная операция (и заслуженно, поскольку значение соединения для обработки реляционных данных трудно переоценить), тем не менее по своей сути оно сводится к последовательности двух других операций, рассмотренных ранее: декартова произведения и выборки. Собственно говоря, по отдельности от соединения я бы затруднился привести пример, где результат декартова произведения сам по себе обладал бы какой-то ценностью. Обычно рассматривают несколько разновидностей соединения, хотя разница между ними не столь велика, и одни разновидности просто являются частным случаем других:
Соединение В общем случае соединение обозначается так: (A TIMES B) WHERE c Обозначение хорошо передает суть операции: на декартово произведение отношений A и B накладывается операция выборки. Пожалуй, повторять здесь требования к исходным отношениям, а также описывать заголовок и тело результирующего отношения было бы тавтологией, поскольку они вытекают из уже рассмотренного ранее. Тэта-соединение Тэта-соединение является частным случаем общего соединения. Если в отношении A имеется атрибут X, в отношении B атрибут Y, а условие c имеет вид X#Y, где # - один из операторов сравнения (=, <>, >, >=, <, <= и т.п.), то результирующая операция называется тэта-соединением. Для нее имеется другое, более компактное обозначение: A [X # Y( B Для примера предположим, что в нашей библиотеке не все читатели обладают равными правами. Есть редкие издания, доступные только ограниченному кругу. У книги есть атрибут ее ценности level, а у читателя некоторый уровень доступа rate, причем читатель не может получить книгу, ценность которой превышает его собственный уровень доступа. Библиотекарь хочет распечатать все возможные комбинации, кому какую книгу можно выдать по этим правилам. Вот решение его проблемы: Readers [rate >= level( Books Возможно, для удобства пользования в дальнейшем библиотекарь подвергнет результат операции проекции, чтобы оставить в отчете только необходимые столбцы Ф.И.О. читателя и Код книги, но сути дела это не меняет. Эквисоединение Эквисоединение тоже частный случай, но уже тэта-соединения. Эквисоединение это тэта-соединение, в котором оператор сравнения обычное равенство. Эквисоединение рассматривается как особая разновидность соединения только потому, что на практике применяется особенно часто. Обозначается эквисоединение, как нетрудно догадаться, так: A [X = Y( B Добавим к таблице Books атрибут givento, содержащий код читателя, которому выдана книга, или пусто, если она в данный момент находится в библиотеке. Потребуем у нашей базы отчет, какие книги в данный момент на руках и у кого: Readers [id = givento( Books Мы начинаем замечать, что реляционная база данных способна не только хранить данные подобно электронной таблице, но и представлять результаты в удобной для пользователя форме, причем запрос зачастую можно представить в виде несложной реляционной операции или их комбинации. Естественное соединение Естественное соединение можно применять к отношениям, имеющим общее подмножество атрибутов. Пусть даны два отношения: A(A1, A2, , Ai, X1, X2, , Xn) и B(X1, X2, , Xn, B1, B2, , Bj). Существует, конечно, формальное определения результата операции естественного соединения, но я в данном случае предпочту представить его как частный случай тэта-соединения: A [A.X1=B.X1AND A.X2=B.X2 AND AND A.Xn = B.Xn] B (правда, в данном случае я немного схитрил: поскольку в отношениях A и B имеются одноименные атрибуты, то, чтобы избежать коллизии имен и не связываться с громоздким переименованием атрибутов, я квалифицировал атрибуты посредством обозначения имя-отношения.имя-атрибута;поскольку статью я ориентировал на программистов, а квалификация известна по крайней мере со времен появления Modula-2 (возможно, и ранее, но мне не встречалась), то уверен, что недоразумений это не повлечет). Словами это можно попытаться представить так: строки из отношения Aсцепляются с теми строками отношения B, для которых значения одноименных атрибутов совпадают. Естественно, что совпадающие атрибуты включаются в результирующее отношение в единственном экземпляре.Обозначается естественное соединение так: A JOIN B Имена атрибутов, по которым производится слияние, не указываются в операции по вполне понятной причине. Примеров естественного слияния приводить не буду, ибо предыдущий пример совсем нетрудно применить к естественному слиянию путем элементарного переименования атрибута. Деление Последняя реляционная операция над отношениями, которую мы рассмотрим, - это деление отношений. Операция эта довольно своеобразна, и простое интуитивное определение для нее мне подобрать не удалось. Придется довольствоваться формальным. Допустим, у нас есть два отношения A(A1, A2, , An, X1, X2, , Xm) и B(X1, X2, , Xm). Результатом деления A на B является отношение с заголовком (A1, A2, , An) и телом, образованным множеством кортежей (a1, a2, , an), при этом для всех кортежей (x1, x2, , xn) из отношения B в отношении A найдется кортеж (a1, a2, , an, x1, x2, , xn). Обозначается такая операция так: A DIVIDEBY B Следует признать, что данное определение не блещет ясностью и элегантностью, и понять его после первого прочтения затруднительно. Поэтому пример в данном случае не будет лишним. Предположим, что в нашей библиотеке библиотекарь аккуратно ведет регистрацию выдачи книг. Для этого в его распоряжении имеется таблица ReaderBookс двумя столбцами: bookid код выданной книги, и readerid код читателя, которому ее выдали. После возвращения книги запись из таблицы не удаляется, так что каждая строка навечно фиксирует факт, что такой-то читатель брал такую-то книгу. Предположим, что книг в библиотеке не так уж много, а читатели обладают редкой жаждой знаний. В таком случае теоретически возможна ситуация, когда наиболее рьяные читатели перечитали все книги, а также когда наиболее интересные книги прочитаны всеми без исключения читателями. Рассмотрим первый случай. Библиотекарь хочет отобрать наиболее активных читателей, прочитавших все книги. Для этого он выдает запрос: (Readers JOIN ReaderBook) DIVIDEBY Books[bookid] Первая операция JOIN дает в результате декартово произведение всех читателей на все коды прочитанных ими книг. Вторая операция (сечение) дает список кодов всех книг в библиотеке. В результате деления мы получаем записи о всех читателях, прочитавших все книги в библиотеке. Аналогичным образом можно найти книги, прочитанные всеми читателями. В завершение следует отметить, что в реальных системах управления базами данных есть альтернативные, более элегантные средства решения подобных задач. Но здесь об этом говорить преждевременно. А операция деления приведена лишь для полноты изложения, чтобы дать читателю представление об основныхреляционных операциях. Послесловие Первоначально я планировал в данной статье дать краткий обзор основных теоретических аспектов реляционных баз данных. Но в ходе работы над ней оказалось, что изложение основ реляционной теории слишком велико по объему и чересчур затянулось по времени. Поэтому я пока решил в данной главе ограничиться основами реляционной алгебры,а продолжить рассмотрение других теоретических аспектов баз данных в следующих статьях. Напоминаю, что свое мнение о содержании статьи, стиле изложения и т.д., а также несогласие по каким-то вопросам или пожелания о содержании следующих статей вы можете изложить здесь. |
| начало | почта | статьи | файлы | ссылки | сайты | RSS | о нас | опубликовать | оформление | авторы | друзья | реклама |