Статья: "Угловой энкодер: устройство и процедуры обработки данных"

Статья

Угловой энкодер: устройство и процедуры обработки данных

Прежде всего мне хотелось бы извиниться перед читателями, ожидающими продолжения статьи "Многозадачность во встроенном приложении", если таковые имеются (постоянно растущий счетчик прочтений свидетельствует о наличии читательского интереса к ней, хотя отсутствие отзывов все же вносит легкую ноту сомнения в этом). Дело в том, что эта и предшествующие ей статьи были замечены, и я получил приглашение поучаствовать в некотором достаточно интересном для меня стартапе, относящемся к автоматизации промышленного оборудования для малого бизнеса. Естественно, я не мог упустить шанс попробовать новые для меня технологии в реальном деле. Продолжение статьи обязательно увидит свет в недалеком будущем, причем теперь будет возможность постепенно смещать акцент от заведомо вымышленных задач в сторону вполне реальных.

В основу настоящей статьи легли материалы из отчета, выполненного автором в ходе предварительных исследований по вышеупомянутому проекту. Выдержка из него, относящаяся к измерению угла поворота вала при помощи энкодера, представлена на суд читателей.

Оглавление

1. Применение углового энкодера
2. Устройство и принцип работы
3. Простейшая процедура обработки сигналов декодера
4. Модификации процедуры
- 4.1. Реакция на оба фронта сигнала A
- 4.2. Симметричная процедура
5. Выводы

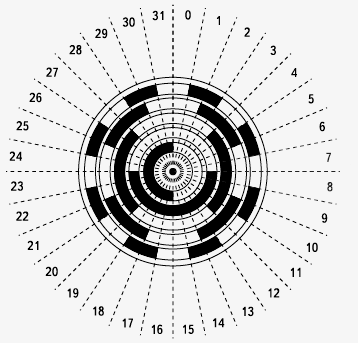
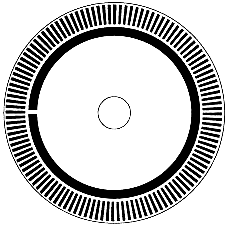
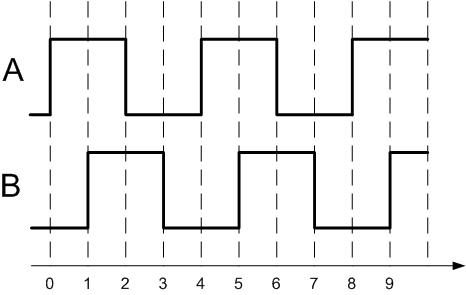
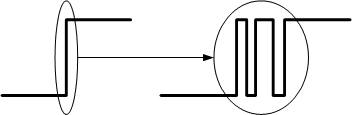
1. Применение углового энкодера

При автоматизации производственных процессов часто приходится решать задачу точного прямолинейного механического перемещения различных узлов автоматизируемой установки (рабочего инструмента станка, координатного стола и т. п.). Одна из простейших реализаций привода для линейного перемещения состоит из вала с нарезанной на нем точной резьбой и гайки, перемещающейся при вращении вала. Если шаг резьбы достаточно равномерный, а люфт гайки невелик, то координата гайки однозначно определяется углом поворота вала относительно некоторого начального положения.

В качестве датчика угла поворота вала можно использовать прибор, называемый угловым энкодером.

2. Устройство и принцип работы

Теоретически принцип работы углового энкодера чрезвычайно прост. Прибор включает жестко закрепленный на валу диск с делениями, каждое из которых однозначно определяет некоторый диапазон положений вала, и устройство для считывания этих делений.

2.1. Способы считывания делений диска

Считывание делений диска может производиться различными способами: механическими контактами (которые размыкаются лепестками на диске), оптическими датчиками (в этом случае диск состоит из чередующихся прозрачных и непрозрачных областей, если считывание производится на просвет, либо отражающих и неотражающих областей, если считывание производится в отраженном свете), магнитными датчиками (например, Холла), электромагнитными и т. п.

Механические контакты подвержены износу (и вследствие этого недолговечны), а в изношенном состоянии еще и склонны к дребезгу, поэтому их применение возможно лишь для некритичных приложений (типа регулировки громкости в музыкальном центре или выбора режима микроволновой печи). Применение их в качестве датчика координаты для станка отпадает.

Магнитные и электромагнитные датчики лишены этих недостатков (во всяком случае, механический износ им не грозит). Однако их изготовление своими руками при приемлемом разрешении довольно проблематично (по крайней мере, мне неизвестны практичные конструкции таких датчиков).

Наиболее пригодными для самостоятельного изготовления при приемлемом качестве представляются оптические энкодеры (этот тезис я намерен в ближайшее время проверить на практике). Впрочем, дальнейшее изложение в равной степени относится к любым способам считывания, разве что при механическом ожидается существенный дребезг контактов.

2.2. Способы кодирования положения диска

Как уже упоминалось ранее, положение (угол поворота относительно некоторого исходного состояния) диска кодируется путем чередования двух типов областей, отчетливо различимых при помощи специальных датчиков (для оптического энкодера это прозрачные и непрозрачные области). Существует два принципиально различных способа такого кодирования: абсолютный и инкрементальный. В соответствии с этим и сами угловые энкодеры можно разделить на абсолютные и инкрементальные.

2.2.1. Абсолютный энкодер

Диск абсолютного энкодера разбивается на некоторое количество секторов (чаще всего, но не всегда, это количество является степенью двойки). Сектора разбиваются на концентрические дорожки, каждая из которых представляет один бит кодированного номера сектора (рис. 1).

Рис. 1. Диск абсолютного энкодера.

В данном примере абсолютный энкодер имеет 32 сектора. Соответственно, для их кодирования нужно log₂(32) = 5 дорожек. Номера секторов обычно задаются кодом Грея. На каждую дорожку диска необходим отдельный датчик.

Код Грея

Тем, кто более-менее знаком с цифровой техникой или основами информатики, привычно двоичное представление целых неотрицательных чисел в виде разложения по степеням двойки:

X = X_n-1*2^n-1 + X_n-2*2^n-2 + ... + X₁*2¹ + X₀*2⁰

Такое представление очень удобно для большинства применений, поскольку совершенно аналогично привычной для нас десятичной записи вплоть до того, что позволяет производить арифметические действия "в столбик" по правилам, известным всем с начальной школы. Оно также легко расширяется и для представления отрицательных чисел в виде "дополнения до двух", что упрощает как аппаратную, так и программную поддержку арифметических операций.

Но все же есть область, где такое представление имеет серьезные недостатки. Эта область связана с кодированием величин в различных датчиках.

Представим себе абсолютный энкодер, к примеру, 8-разрядный (угловой или линейный - не имеет значения). Он отслеживает перемещение по нарастанию координаты:

X	Binary
0	00000000
1	00000001
2	00000010
...	...
126	01111110
127	01111111
128	10000000

На середине шкалы, при переходе от значения 127 к 128, на выходе энкодера меняются одновременно все разряды. В идеальном мире в этом нет ничего страшного. В реальном двух совершенно одинаковых датчиков не бывает, все они хоть немного отличаются друг от друга чувствительностью, быстродействием и т.д.; к этому добавляется неидеальность юстировки при расположении восьми датчиков в линейку. Это приведет к тому, что в процессе перехода от значения 127 (01111111) к 128 (10000000) мы ожидаем увидеть любое 8-разрядное двоичное число (и увидим воочию, если переход выполняется достаточно медленно).

Этот эффект может иметь крайне негативные последствия.

Предположим, что энкодер стоит в системе управления точным приводом. Контроллер, реализующий управление посредством петли обратной связи, сравнивает координату с датчика с желаемым положением инструмента и управляет сервомотором, перемещающим инструмент. Привод получает команду позиционирования в точку 128. Он успешно доезжает до 127 и на минимальной скорости, чтобы не проскочить по инерции, преодолевает последнюю ступеньку до 128.

В этот момент энкодер выдает какое-то случайное значение координаты; контроллер принимает его за истинную координату, вычисляет смещение относительно желаемой позиции и подает соответствующую команду сервомотору для сокращения этого смещения. Это "фантомное" смещение случайно и может быть любым в диапазоне от 0 до половины длины всей линейки (с учетом того, что мы уже находимся в середине; возьмем среднее значение в четверть линейки как наиболее вероятное).

Итак, не доехав до желаемого положения каких-то полшага, сервомотор делает мощный рывок и пытается утащить каретку куда-то в сторону на четверть линейки. По пути датчик "приходит в себя", вычисленное смещение резко уменьшается, и дальнейшее поведение привода полностью зависит от его динамики: тяжелая и медленная каретка просто не успеет разогнаться, легкая же и быстрая может начать осциллировать вокруг точки назначения.

Всех этих неприятностей можно легко избежать, если использовать для представления координаты код Грея. Основная его особенность состоит в том, что при увеличении или уменьшении величины на единицу код Грея для этой величины изменяется лишь в одном разряде:

N	Двоичный код	Код Грея
0	000	000
1	001	001
2	010	011
3	011	010
4	100	110
5	101	111
6	110	101
7	111	100

(такую таблицу можно построить для любого числа разрядов).

Какую бы строку в таблице мы ни выбрали, при переходе на одну строчку вверх или вниз в коде Грея меняется лишь один разряд; следовательно, даже при наличии переходных процессов в датчике разница между двумя отсчетами не превысит одной единицы, что является вполне допустимым в промежуточной зоне.

Для применения кода Грея осталось лишь научиться переводить числа из этой кодировки в "обычную" и обратно, поскольку типичные процессоры этого не умеют. Эти процедуры достаточно просты; я не буду приводить их здесь, поскольку тема весьма популярна, и читатели найдут их без труда. При желании очень легко вывести их самостоятельно, заметив простую закономерность построения кода Грея.

2.2.2. Инкрементальный энкодер

Как следует из самого названия, инкрементальный энкодер определяет не абсолютное положение диска в пределах полного оборота, а относительное смещение от предыдущего положения. Для этого достаточно диска с единственной дорожкой (рис. 2).

Рис. 2. Диск инкрементального энкодера

Часто добавляют вторую дорожку с единственным делением на полный оборот. Эта дорожка позволяет выставить диск в начальное положение, относительно которого впоследствии будут производиться отсчеты. Она также может оказаться полезной в процессе диагностики энкодера, позволяя проконтролировать количество импульсов, выдаваемое датчиком за один оборот диска.

Подсчитывая количество импульсов от датчика, можно определить угол поворота диска относительно предыдущего положения; однако невозможно определить направление вращения диска. Для определения направления используется второй датчик, смещенный относительно первого на четверть шага (половину ширины штриха или промежутка между ними). По разности фаз сигналов датчиков определяется направление вращения диска (подробнее далее).

2.3. Сравнение абсолютного и инкрементального энкодеров

Обе разновидности углового энкодера имеют свои достоинства и недостатки.

Абсолютный энкодер можно опрашивать в любой момент, когда потребуется узнать положение диска, а не обрабатывать перемещение на каждый шаг. Это упрощает работу с ним (в частности, делает тривиальным определение направления вращения диска), а также снижает требования к контроллеру, обрабатывающему данные о координатах (если контроллер потеряет несколько импульсов от датчиков, информация о текущем положении диска все равно будет доступна).

К недостаткам абсолютного энкодера в первую очередь следует отнести сложность изготовления, связанную с наличием большого числа датчиков (по одному на каждую дорожку диска, то есть на каждый разряд кода угловой координаты диска). Также в случае высокой точности энкодера (и, как следствие, большого количества разрядов данных) для подключения энкодера к контроллеру потребуется большое число линий связи и такое же число битов ввода (в случае параллельной передачи данных) либо затраты на дополнительное оборудование сериализации (в случае последовательной передачи).

В случае инкрементального энкодера достоинства и недостатки меняются местами по сравнению с абсолютным. Достоинствами являются: простота (всего два датчика вне зависимости от разрешения), относительная легкость при кустарном изготовлении, малое количество линий связи с контроллером. Недостатки: высокие требования к быстродействию контроллера (в случае потери импульсов от датчиков в данных о координате будет накапливаться ошибка), более высокая сложность обработки данных (из-за необходимости определения направления вращения диска).

Поскольку программировать мне гораздо привычнее, чем изготавливать точную механику, а быстродействие примененных в проекте микроконтроллеров AVR более чем достаточно для такой задачи, то достоинства инкрементального энкодера в данном случае превысили его недостатки, поэтому выбор между возможными вариантами был сделан в его пользу.

Далее речь пойдет исключительно об инкрементальном декодере, поэтому тип энкодера я больше уточнять не буду.

3. Простейшая процедура обработки сигналов декодера

Прежде чем приступить к рассмотрению процедур обработки сигналов декодера, выясним, что представляют собой эти сигналы.

Как уже говорилось ранее, декодер имеет два датчика: A и B. Датчики сдвинуты друг относительно друга на половину ширины штриха (или четверть шага диска), поэтому сигналы получаются сдвинуты по фазе на p/2. Примем для определенности, что сигнал B отстает от сигнала A при повороте диска против часовой стрелки:

Рис. 3. Форма сигналов датчиков A и B

Из рис. 3 видно, что при движении диска против часовой стрелки (состояния 0-1-2-3-4...) в момент перехода сигнала A из состояния 0 в 1 (передний фронт) сигнал B всегда находится в состоянии 0 (см. состояния 0, 4, 8). Если же диск движется по часовой стрелке (7-6-5-4-3...), сигнал B всегда находится в состоянии 1 (состояния 6, 2).

Отсюда вытекает простейшая процедура обработки сигналов декодера: по переднему фронту сигнала A проверить состояние сигнала B; если он равен 0, увеличить счетчик координаты на единицу, в противном случае уменьшить его на единицу.

Эта процедура применяется в подавляющем числе конструкций, опубликованных в интернете. Он вполне пригоден для применения в некритичных устройствах, когда погрешность определения координаты не приводит к фатальным последствиям: не так давно вытесненные оптическими роликовые мыши/трекболы, валкодеры магнитол и т. п. Однако он не годится для применений, в которых точность определения координаты является решающим фактором, например, в системах ЧПУ.

Причина несовершенства такой, казалось бы, простой и надежной процедуры кроется в том, что он требует сигналов идеальной формы. В реальных условиях датчики могут иметь «дребезг» при смене состояния сигнала (особенно это относится к датчикам с механическими контактами). В этом случае вместо четкого перехода 0→1 на осциллограмме сигнала мы увидим последовательность из нескольких быстрых переходов:

Рис. 4. Дребезг сигнала

В результате дребезга приращение координаты будет произведено несколько раз вместо одного, и значение координаты будет безнадежно испорчено.

Для борьбы с дребезгом применяются разнообразные методы. Большинство из них примитивны и сводятся скорее к «заметанию мусора под ковер» — от аппаратного подавления дребезга фильтром НЧ (RC-цепью) до запрета реакции на последующие переходы сигнала до истечения некоторого тайм-аута, в течение которого, по замыслу авторов, дребезг должен заведомо прекратиться.

Этот подход представляется неубедительным, поскольку основан на компромиссе: если тайм-аут окажется слишком коротким, остается риск, что дребезг будет принят за действительный сигнал; если же для надежности сделать его слишком длинным, есть опасность потерять действительные импульсы при быстром движении диска. Таким образом, решение оказывается слишком тесно привязанным к свойствам конкретного датчика и плохо масштабируемым по скорости вращения диска.

Впрочем, даже если бы удалось избавиться от дребезга полностью, проблема все равно не была бы решена. Предположим, что диск находится в положении между точками 3 и 4 на рис. 3 (назовем такую точку 3.5). При перемещении в точку 4.5 в точке 4 сигнал A переходит из 0 в 1, и согласно нашей процедуре координата диска увеличивается на единицу (поскольку сигнал B равен нулю на переднем фронте импульса A). Затем диск возвращается из 4.5 обратно в 3.5, но, поскольку при обратном движении диска в точке 4 сигнал A переходит из 1 в 0, наша процедура игнорирует это событие.

Итак, имеем: диск переместился на небольшой угол и вернулся в исходное положение, а координата увеличилась на единицу. Можно повторять такое перемещение произвольное число раз, и координата каждый раз будет увеличиваться. В итоге координата диска, измеренная посредством простейшей процедуры, не будет иметь ничего общего с истинным положением диска.

Аналогичная проблема возникнет в случае, если диск будет совершать колебания между точками 5.5 и 6.5, только в этом случае измеренное значение координаты будет уменьшаться.

Проблема является достаточно актуальной, поскольку вероятность остановки диска на границе между светлой и темной зонами достаточно велика, а вибрации при работе промышленного оборудования в сочетании с возможным люфтом привода вполне могут привести к колебаниям диска, достаточным для смены состояния датчика A. Это делает простейшую процедуру обработки сигналов по переднему фронту сигнала A непригодной для ответственных применений, где требуется максимальная точность измерения координаты диска.

4. Модификации процедуры

Для повышения достоверности данных о координате диска процедуру обработки данных следует модифицировать. Далее приведены два варианта модифицированных процедур.

4.1. Реакция на оба фронта сигнала A

Как мы видели ранее, причиной некорректного результата простейшей процедуры являлась его реакция лишь на передний фронт сигнала A. По этой причине процедура «не замечала» обратного отката диска и не корректировала координату в сторону уменьшения.

Наиболее очевидный способ устранить эту ошибку — заставить процедуру реагировать на оба фронта сигнала A:

1. Дождаться фронта сигнала A.
2. Если сигнал B = 1, перейти к шагу 1.
3. Если фронт сигнала A передний, увеличить координату на единицу, иначе уменьшить координату на единицу.
4. Перейти к шагу 1.

Наша модифицированная процедура реагирует на фронты сигнала A, приходящиеся на нулевое состояние сигнала B. Для повышения разрешающей способности энкодера вдвое мы можем доработать ее таким образом, чтобы использовались все фронты сигнала A:

1. Дождаться фронта сигнала A.
2. Если фронт сигнала A передний, то
- 2.1. если сигнал B = 0, то увеличить координату на 1, иначе уменьшить координату на 1;
- 2.2. перейти к пункту 1.
3. Если сигнал B = 1, то увеличить координату на 1, иначе уменьшить координату на 1.
4. Перейти к пункту 1.

У данной процедуры остается одна уязвимость: если для реакции на фронты сигнала A используется прерывание, на время его обработки контроллер перестает реагировать на другие фронты, что может привести к ошибке при наличии дребезга сигнала. Поэтому потребуется либо установить фильтр низких частот на входе прерывания по смене состояния сигнала A (с постоянной времени больше, чем время обработки прерывания), либо отказаться от прерываний вовсе и опрашивать состояние обоих сигналов по таймеру. Во втором случае следует аккуратно выбрать частоту таймера, чтобы не происходила потеря импульсов при быстром движении диска.

4.2. Симметричная процедура

В предложенных ранее процедурах сигнал A использовался в качестве основного, сигнал B — в качестве вспомогательного. Все события отслеживались только на канале A. На самом деле деление сигналов на A и B условно, они вполне взаимозаменяемы. Попробуем отойти от такого искусственного деления и рассмотреть сигналы как равноправные:

№	A	B
0	0	0
1	1	0
2	1	1
3	0	1
4	0	0
5	1	0
6	1	1
7	0	1
8	0	0

Табл. 1. Состояния сигналов A и B при вращении диска против часовой стрелки

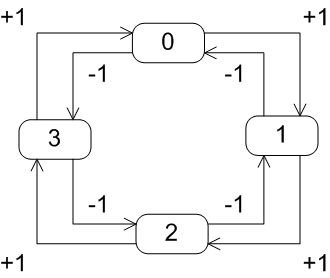
Если рассмотреть комбинацию значений <BA> как двухразрядное двоичное число, получаем циклическую последовательность: 00 — 01 — 11 — 10 — 00 …

В обычном двоичном представлении, когда каждый разряд представляет соответствующую ему степень двойки, эта последовательность интерпретируется как 0 — 1 — 3 — 2 — 0 … и не несет большого смысла. Но если рассмотреть эту последовательность как код Грея, она представляется гораздо более осмысленной: 0 — 1 — 2 — 3 — 0 … Соответственно, при обратном направлении вращения диска (по часовой стрелке) эта последовательность принимает вид 0 — 3 — 2 — 1 — 0 …

Такие последовательности очень похожи на смену состояний некоего конечного автомата:

Рис. 5. Диаграмма состояний конечного автомата

В данном случае получилась своеобразная «автоматная модель наоборот»: обычная модель показывает переходы и действия, которые моделируемый автомат произведет при подаче на него соответствующих сигналов; в нашем случае действия производятся по факту состоявшегося перехода.

Для программной реализации процедуры отсчета координаты удобно воспользоваться табличным представлением диаграммы переходов:

	0	1	2	3
0	-	-1	X	+1
1	+1	-	-1	X
2	X	+1	-	-1
3	-1	X	+1	-

Табл. 2. Табличное представление диаграммы состояний

Здесь:

строки — текущее состояние пары сигналов <BA>;
столбцы — предыдущее состояние пары сигналов <BA>;
«-» — состояние сигналов не изменилось, никаких действий;
«X» — запрещенный переход, свидетельствующий о потере данных;
«+1» — увеличение координаты на единицу;
«-1» — уменьшение координаты на единицу.

Достоинства процедуры: простота реализации; способность обнаруживать потерю импульсов.

Недостатки: в случае работы по прерываниям задействуются два входа внешних прерываний контроллера, что может оказаться излишне расточительным; кроме того, в отсутствие аппаратного подавления дребезга фильтром нижних частот возможна слишком высокая частота прерываний с возможной потерей некоторых импульсов (и, как следствие, потерей точности измерения координаты).

5. Выводы

Наиболее практичным для малобюджетных проектов датчиком координаты представляется угловой инкрементальный энкодер с оптическими датчиками.
Для программной обработки данных, поступающих от энкодера, целесообразно применять симметричную процедуру (см. п. 4.2).

Версия для печати

Обсудить на форуме (67)